Miscellaneous mathematical stuff that I found interesting at one point
or another.
Where there is math writen on these pages it is constructed using
MathJax, a lovely little Javascript library just for this.
To get to play with it, I borrowed the scripts to set up a little
dynamic LaTeX box. Have a look here http://bandicoot.maths.adelaide.edu.au/MathJax/test/sample-dynamic-2.html.
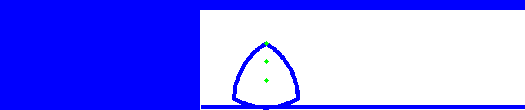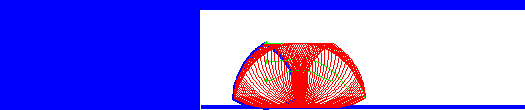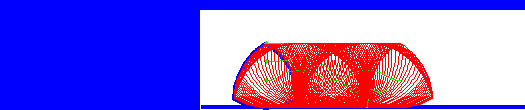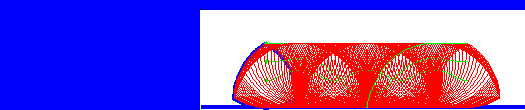
A Reuleaux triangle
is the shape you get, starting from an equilateral triangle, and
adding three circular arcs, drawn from each corner. It’s not actually
a triangle, but what’s in a name?
The interesting thing is that a Reuleaux triangle is a shape of
constant width. That means it can be used as a roller (but not a
wheel). The animation below shows this – we can see that although the
centre of the triangle moves up and down, the top surface of the
rotating triangle is always level.
Follow the link below to see more, get links to 3D printable versions,
and Matlab code to play with it.
A couple of little tools for playing with Catenaries can be found at:
http://bandicoot.maths.adelaide.edu.au:3838/catWorkshop/,
and http://bandicoot.maths.adelaide.edu.au:3838/catenary/. They
aren’t really documented yet – they’re just a toy to play with Shiny – but more will come
later.
Leslie Matrices are a tool for modelling population demographic
dynamics. Wikipedia
does a decent job of explanation of these. My megre contribution
is a little online
Leslie Matrix Calculator.
A Log-azimuthal map of the world (as seen from Adelaide, Australia,
my home town) using log-distances, is a map that shows places close
by are displayed in detail, and those further away, have less.
There are a large variety of sea-shells (and land shells) that can be
simply described by rotating a ellipse around a log-spiral that has
been projected onto a cone. The image below was generated using this
approach:
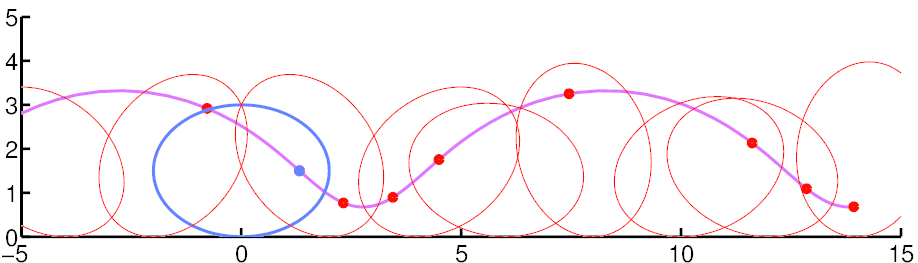
A Roulette is a curve
derived by rolling one curve against another. In the image below, the
blue point on the blue ellipse is rolled along a straight line (the
x-axis) to generate the purple curve (which is called an
undularly).
Included here is some Matlab code to generate roulette curves, with a
fair degree of generality, but also showing how to generate specific
instances such as cycloids, trochoids, the Cissoid of Dioclese, and
the undularly and nodary.





